Straightening of Railway Curves - Field work -Trabajo de campo

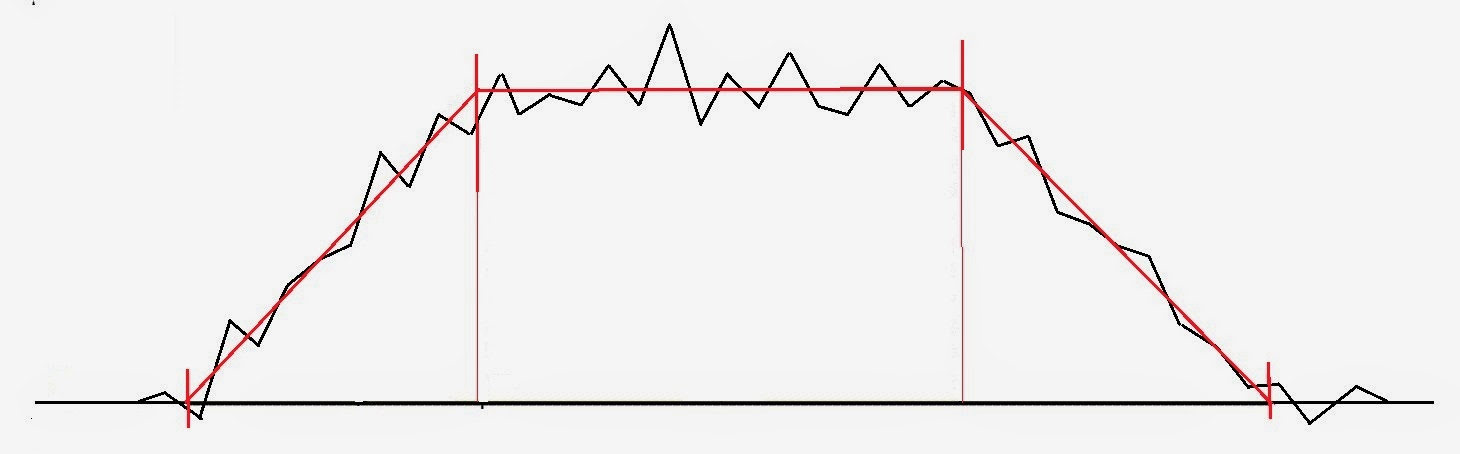
Measurement of the railway.

In the railway, the rail is referenced by kilometrical and heptametrical points (PK and PH).  

These PKs refer typically to the axis of the railway in case we work with a single railway, or to the axis of the gauge if we have a double-railway.

But we are especially interested in knowing the status of the outer rail of the railway (driver rail). For this purpose we will measure and mark such rail, where we will collect the data of the sagittas.

Marking of the outer rail

Starting from a defined straight-alignment and a real known kilometric point (hereinafter PKr), we will start drawing the head of the rail by its outer side, from approximately 50m before the curve with a mark each 10m and up to approximately 50m after the curve.

We will number the points from “0” in the starting PKr, marking the “mark points” (PKm): : the “1” to 10 m, the “2” to 20 m, etc. stressing the marks each 50 and 100m in order to facilitate the double-check.

The last point “n” will have a mark point (PKm) and a real mark (PKr). 

The difference between the PKr and the PKm of the measured point “n” will be known as “gap”.

Data of the references

All the references must be defined by a name (mast, wall, etc.), its PK and its situation with regards to the railway (left (Dr)/ right(Iz)).

Once we have marked the curve we will define the longitudinal distance (L) at which the points marked in the rail are placed and the perpendicular distance to the closest rail (d).

In case of being working with a double-railway, we will also take as references some distances to the gauge in front of the marked points.

Alignment of straight-lines

Starting from a defined point of a straight-line and placing the tachymeter over the active face of the rail (or in a parallel to it), we will define the definitive alignment of the straight-line, taking the data of the distance from this alignment to the reference-points. 

In the marking points (0), (1) and (2) as well as in the last points  (n-2), (n-1) and (n) we will take the distance existing from the alignment of the straight-line defined by the tachymeter and the active face of the rail in those points, giving positive value if the separation is placed between the straight-line and the center of the curve, and negative value if it is placed oppositely.

We will call these distances: D₀, D₁, D₂ y  D_n-2, D_n-1, D_n 

Sagittas of the curve

Using the “sagitta handles” (as those shown in the picture below), we will place the first handle over the marking-point “0” and the second handle over the point “2”, stretching out the nylon-chord perfectly (taking care of not touching any obstacle), and we will measure the sagitta of the point “1”.

This kind of handles allow to separate the nylon 2cm from the active face of the rail in order to measure negative sagittas, and therefore we must subtract the 2cm to the measured sagitta.

Then we keep forward with the first handle to the point “1” and the second handle to the point “3”, measuring the sagitta of the point “2”.

We will keep measuring until having the first handle over the point “n-2” and the second over the point “n”, measuring the sagitta of the point “n-1”.

All the data collected will be reflected in a document, similar to the one below:

Curve straightening

Before starting straightening a curve we must ensure that the curve is tangent to the straight-lines before and after it.

For this purpose we will use the data collected in the line alignment (D₀, D₁, D₂) and (D_n-2, D_n-1, D_n), as well as the sagittas taken in the points (1, 2) y (n-1, n).

The first Sagitta Law states: 

F₂= f₂ + D₂ - (D₁/2) - (D₃/2)

Each “D” with its sign;  “+” out, “-” in

A corrected sagitta (F) is equal to the measured sagitta (f) + (the displacement in this point with the corresponding sign) – ( semi-displacement of the point immediately before with the corresponding sign) - (semi-displacement of the point immediately after with the corresponding sign).

• The sagitta in the point (0) is noted as (“0”): F0=0 
• In the point (1) it will be : F1=f1 + D1- (D0/2) - (D2/2) 
• The new sagitta in the point (2) will be: F2=f2 + D2 - (D1/2) 
• The new sagitta in the point (3) will be: F3=f3 - (D2/2)

With this calculation we have created a line between the points (0) and (2).

We will do the same in the exit line:

• The new sagitta in the point (n-3) will be: Fn-3=fn-3-(Dn-2/2) 
• In the point (n-2) it will be: Fn-2 = fn-2 + (Dn-2)- (Dn-1/2) 
• In the point (n-1) it will be: Fn-1=fn-1+Dn-1- (Dn-2/2)-Dn/2 
• And the sagitta in the point (n) will be noted as (“0”): Fn=0

Taking into account ALWAYS the sign of the displacements.

With this calculation we have created a line between the points (n-2) and (n).

These new sagittas (F₀, F₁, F₂) and (F_n-2, F_n-1, F_n) will replace the sagittas really measured in the document, writing as well the displacements (D_o, D₁) and (D_n-1, D_n) in order to add them to the results of the calculation.

So now we have all the necessary data to straighten the curve:

• The curve is tangent to all adjacent lines 
• We have measured all the sagittas of the curve 
• We have placed all the references over with we will materialize the design 

Now we will see some features of the curves and the sagittas.

 If we increase the displacements in a curve, then we will increase the sagitta or, which is the same, we will reduce the radius. If we reduce the displacements, we will reduce the sagitta or, which is the same, we will increase the radius.

The total angle of the curve (α) is always the same.

Its gravity center does not vary with one or other radius, as far as the entry and exit transitions remain the same.

The addition of the measured sagittas and the additions of the calculated sagittas, will be always the same regardless the radius.

The addition of the differences between the measured sagittas and the calculated sagittas will be 0. 

GO TO CHAPTER VII - Alignment and Leveling of Railroad with Heavy Machinery

Full themes in the book -In paper and ebook (Follow the link)

------------------------------------------------

Medición de la vía.

En el ferrocarril la vía está referenciada por puntos kilométricos y hectométricos.

Estos PKs se refieren generalmente al eje de la vía en el caso de tratarse de una vía única o al eje de la entrevía en el caso de tratarse de vía doble.

A nosotros nos interesa conocer el estado del carril exterior de las curvas “carril director”. Para ello mediremos y marcaremos dicho carril, donde tomaremos los datos de las flechas.

Marcado del carril exterior

Partiendo de una alineación recta definida y de un punto kilométrico real (PKr) conocido, se comenzará a pintar en la cabeza del carril por el lado exterior, desde aproximadamente 50 m. antes de la curva con una marca cada 10 m. hasta aproximadamente 50 m. después de terminar la curva.

Numeraremos los puntos desde el punto “0” en el Pkr del comienzo, marcaremos los puntos de marcaje (PKm) : el “1” a 10 m, el “2” a 20 m, etc. Distinguiendo las marcas cada 50 y 100 ml, para facilitar la comprobación.

Al último punto “n” le corresponderá un PK medida (PKm) y un PK real del trazado (PKr).

La diferencia entre el (PKr) y el (PKm) del punto medido “n” la llamamos desfase.

Datos de las Referencias

Todas las referencias las tenemos que definir por un nombre (poste, muro, etc.), su (PK), y su situación respecto a la vía (Dr/Iz)

Una vez marcada la curva definiremos a qué distancia en posición longitudinal (L) se encuentra de los puntos marcados en el carril y a qué distancia en perpendicular se encuentra el carril más próximo (d)

Caso de estar trabajando en un trayecto de doble vía, tomaremos también como referencias algunas distancias de entrevía frente a los puntos de marcaje.

Alineación de las rectas

Partiendo de un punto definido de una recta y situando el taquímetro sobre la cara activa del carril o en una paralela a este, definiremos la alineación definitiva de la recta, tomando datos de la distancia que existe de esta alineación a los puntos de referencia.

En los puntos de marcaje (0), (1) y (2) así como en los últimos puntos (n-2), (n-1) y (n) tomaremos la distancia que existe entre la alineación de la recta definida por el taquímetro y la cara activa del carril en esos puntos, dando valor positivo si esta separación está situada entre la recta y el centro de la curva o negativo si está situada en el otro sentido.

A estas distancias las llamaremos D0, D1, D2 y Dn, Dn-1, Dn-2

Flechado de la curva

Utilizando las “Asas de flechar”, colocaremos la primera “asa” sobre el punto de marcaje “0”, y la segunda “asa” sobre el punto “2”, extendiendo perfectamente el nylon que las une (teniendo cuidado de que no roce sobre ningún obstáculo), mediremos la flecha en el punto “1”.

Este tipo de asas, separan el nylon 2 cm de la cara activa del carril para poder medir las flechas negativas, por lo tanto a la flecha medida habrá que restarle esos 2 cm.

A continuación avanzamos la primera asa hasta el punto “1” y la segunda hasta el punto “3” midiendo la flecha en el punto “2”

Seguiremos hasta tener situada la primera asa sobre el punto “n” y la segunda sobre el punto “n-2”, donde mediremos la flecha del punto “n-1”.

Todos los datos tomados se reflejarán en un impreso.

Rectificación de curvas.

Antes de comenzar a rectificar la curva, debemos asegurarnos que la curva sea tangente a las rectas anterior y posterior.

Para ello utilizaremos los datos tomados en la alineación de las rectas (D0, D1, D2) y (Dn-2, Dn-1, Dn), así como las flechas tomadas en los puntos (1, 2) y (n-1, n).

La primera ley de las flechas dice: 

F2=f2 + D2 - (D1/2) - (D3/2) 

Cada “D” con su signo; “+” a exterior, “-” a interior 

Una flecha corregida (F) es igual a la flecha medida (f) + (desplazamiento en ese punto con su signo) – (semidesplazamiento del punto anterior con su signo) - (semidesplazamiento del punto posterior con su signo)

• La flecha del punto (0) la anotamos como (0): F0=0
• En el punto (1) será : F1=f1 + D1- (D0/2) - (D2/2)
• La nueva flecha en el punto (2) será: F2=f2 + D2 - (D1/2)
• La nueva flecha en el punto (3) será: F3=f3 - (D2/2)

Con este cálculo hemos creado una recta entre los puntos (0) y (2)

En la recta de salida haremos lo mismo:

• La nueva flecha en el punto (n-3) será: Fn-3=fn-3-(Dn-2/2)
• En el punto (n-2) será: Fn-2=fn-2 + (Dn-2)- (Dn-1/2)
• En el punto (n-1) será: Fn-1=fn-1+Dn-1- (Dn-2/2)-Dn/2
• La flecha del punto (n) la anotamos como (0): Fn=0

Teniendo siempre en cuenta el signo de los desplazamientos.

Con este cálculo hemos creado una recta entre los puntos (n-2) y (n)

Estas nuevas flechas (F0, F1, F2) y (Fn-2, Fn-1, Fn) sustituirán en el impreso de medición a las flechas realmente medidas, anotando también los desplazamientos (Do, D1) y (Dn-1, Dn) para luego sumarlos a los resultantes del cálculo.

Ya tenemos todos los datos necesarios para poder rectificar la curva:

• La curva es tangente a las rectas adyacentes
• Hemos tomado todas las flechas de la curva
• Tenemos situadas las referencias sobre las que materializaremos el trazado.

Vamos a ver ahora algunas características de las curvas y las flechas.

• Si en una curva aumentamos los desplazamientos, aumentamos la flecha o lo que es lo mismo, disminuimos el radio, si disminuimos desplazamientos, disminuimos la flecha y aumentamos el radio.
• El ángulo total de la curva (α) es siempre el mismo.
• Su centro de gravedad no varía con uno u otro radio, si las transiciones de entrada y salida tienen el mismo valor.
• La suma de las flechas medidas y la suma de las flechas calculadas, será siempre la misma con cualquier radio.

La suma de las diferencias entre las flechas medidas y calculadas es (0).


IR A CAPÍTULO VII - Alineación y Nivelación de Vía con Máquina Pesada.

Temas completos en el libro - en papel y ebook (Siga este enlace)

Straightening of Railway - Introduction - Introducción

If we link two points of a curve with a chord, we name “sagitta” (f) the distance from the center of the chord to the intersection point between the perpendicular to the chord and the curve.

If we take always the same chord length and we measure the sagitta in its center, the same sagitta will correspond always to the same radius.

If we consider the straight-line as a curve with infinite radius, its sagitta will be “0”. 

If we know the length of the chord and the length of the sagitta, we can likewise calculate the radius of the curve.

Formulae of the chord, arc and sagitta

In a circumference of center O and radius R, we draw the chord AB =2c, being M the mid-point of such chord.

The diameter drawn CMOD is perpendicular to the chord AB in the point M, being the sagitta: f = MC

Using the triangle similarity: CMB and DMB

CM/MB = MB/MD ;CM*MD = MB*MB

And replacing values: CM = f;      MD = (2R - f)

Therefore:   C ²=f*(2R-f)= 2*R*f – f ²

In railways, the radiuses of the curves are very large with regards to their sagittas, since we use chords of 20m, and therefore we can disregard the term f ²:

C ²=2*R*f

f = C ² /2*R

For chords of 20 m,    c = 10 m.    We obtain:

f = 50 /R or  f = 50.000/R (f in mm, R in mts) 

The relation between the length of the arc (S), the sagitta (f) and the chord (C) is as follows:

S=2*((f/2)+(C² /(2*f)))*ASN ((8*f*C)/(f ²+ C² ))

In the curves, the train circulates guided by the outer rail, also known as driver-rail, in which the flange of the wheel attacks the rail with an angle variable as a function of the curve radius.

In order to avoid abrupt direction changes, the curvature must be uniform.

Abrupt direction changes caused by significant curvature differences will entail knocks in the rail that little by little will cause deformations in the railway and, the bigger the deformation, the bigger the knock, making the deformation grow exponentially.    

Since the sagittas of the curve will indicate its curvature, their values must be identical in the circular curve, and the variation required when passing from straight-line to curve (or reversely) must be smooth and progressive.

Using the clothoid as transition curve, in which the main property was that its curvature is proportional to its length, we ensure a uniform progression for the sagitta changes.

A curve can be represented, as commented before, by its sagitta diagram, and its perfect status would have the following shape:

In the circular curve the sagitta will be equal in each of its points, and in the transitions it will be increasing or reducing progressively. 

In the railway, deformations in the curvature occur with the course of time and motivated by the 

following factors:

• Circulation at inappropriate speed 
• Dilatations due to temperature changes 
• Ballast-base displacement due to rainfalls 
• Etc. 

These deformations cause consequently variations in the sagittas, so the sagitta diagram can become something like:

Since the differences in the curvature will entail that the deformations increase more and more rapidly, it is essential to correct periodically the curve to bring it back to its primitive status.

This correction process is also known as “Curve straightening”.

The process of curve straightening must be carried out, not only for the maintenance of a ballasted railway, but it is also essential to carry it out before pouring the concrete on a ballastless (concrete slab)-railroad, in order to “round off” the polygonal-path that we have created in a coordinates setting-out so that we minimize the assembly-mistakes.

It will be composed of the following phases:

1.- Field work

• Measurement of the railway 
• Data collection from existing references. 
• Alignment of adjacent lines. 
• Sagittas of a curve 

2.-Desk work

• Manual or computer straightening 
• Calculation results in paper. 

3.-Materialization of the straightened design.

• Place the calculation data in the respective references
• Submittal of the calculation results to the staff responsible of maintenance with heavy machinery.

GO TO CHAPTER VI- Straightening of Railway-  Field work

Full themes in the book -In paper and ebook (Follow the link)

----------------------------------------------------------------

INTRODUCCIÓN

Si unimos dos puntos de una curva con una cuerda, denominaremos flecha a la distancia que hay entre el centro de la cuerda y su perpendicular en la curva.

Si tomamos siempre la misma longitud de cuerda y medimos la flecha en el centro de esta, a un mismo radio corresponderá siempre una misma flecha.

Si consideramos una recta como una curva de radio infinito, su flecha será “0”

Si conocemos la longitud de la cuerda y la medida de la flecha, podemos conocer el radio de una curva.

Repaso de fórmulas

En una circunferencia de centro O y radio R, se traza la cuerda AB = 2c, siendo M el punto medio de dicha cuerda.

El diámetro trazado CMOD es perpendicular a la cuerda AB en el punto M, siendo la flecha: f = MC

Por semejanza de triángulos: CMB y DMB

CM/MB = MB/MD ; CM x MD = MB x MB

Reemplazando valores: CM = f ; MD = (2R - f)

Luego:   C 2 = f x (2R-f)= 2Rf – f 2
 
En ferrocarriles, los radios de las curvas son muy grandes en relación a las flechas, pues se utilizan cuerdas de 20 m, pudiendo despreciar el término  f 2

C 2= 2Rf

f = C 2 /2R

para cuerdas de 20 m,    c = 10 m. Resulta:

f = 50 /R o bien f = 50.000/R (f en mm, R en mts)

La relación entre la longitud de arco (S), la flecha (f) y la cuerda (C) es la siguiente

           S=2 x ((f/2)+(C2 /(2 x f))) x  ASN ((8 x f x C)/(f 2+ C2 ))

En las curvas, el tren circula guiado por el carril exterior, llamado carril director, en el que la pestaña de la rueda ataca al carril con un ángulo variable en función del radio de la curva.

Para que no existan cambios de dirección bruscos, la curvatura debe ser uniforme.

Los cambios bruscos de dirección motivados por una diferencia de curvatura importante producirán golpes en el carril que poco a poco irán deformando la vía y a mayor deformación, mayor será el golpe y la deformación se hará exponencial. 

Como las flechas de la curva nos indican su curvatura, estas deberán ser uniformes en la circular y la variación necesaria al pasar de recta a curva o viceversa deberá ser suave y progresiva.

Utilizando como curva de transición la clotoide, que entre sus propiedades está la de que su curvatura es proporcional a su longitud, nos aseguramos la progresión uniforme en el cambio de flechas. 

Una curva se puede representar por su diagrama de flechas, y su estado perfecto tendrá la siguiente forma:

En la circular la flecha será igual en todos sus puntos, y en las transiciones irán aumentando o disminuyendo de forma progresiva. 

En una línea férrea, con el paso del tiempo y motivado por distintos factores:

• Circulación a velocidad inadecuada. 
• Dilataciones por cambios de temperatura. 
• Descalces del balasto por lluvias. 
• Etc. 

Se producen deformaciones en la curvatura y por lo tanto una variación en las flechas, de manera que el diagrama de flechas puede quedar de una forma similar a este:

Como las diferencias en la curvatura harán que cada vez se vayan incrementando las deformaciones más rápidamente, es indispensable que periódicamente se corrija la curva para volverla a su estado primitivo. 

A este proceso de corrección lo denominamos “Rectificación de Curvas”.

El proceso de rectificación de curvas se debe realizar, no solo para el mantenimiento de una vía sobre balasto sino que también es indispensable realizarla antes de hormigonar una vía en placa, para “redondear” la poligonal que hayamos creado en un replanteo por coordenadas.

Consta de las siguientes fases:

1.- Trabajo de campo 

• Medición de la vía. 
• Toma de datos de las referencias existentes. 
• Alineación de las rectas adyacentes. 
• Flechado de la curva. 

2.-Trabajo de oficina 

• Rectificación manual o mediante programa informático. 
• Obtención en papel de los resultados del cálculo. 

3.-Materialización del trazado rectificado. 

• Colocar los datos de cálculo en las referencias. 
• Entrega a los responsables de mantenimiento con la maquinaria pesada de los resultados del cálculo.

IR A CAPÍTULO VI - Rectificación de Curvas Ferroviarias - Trabajo de campo

Temas completos en el libro - en papel y ebook (Siga este enlace)